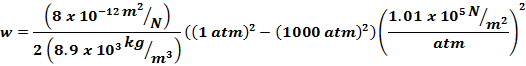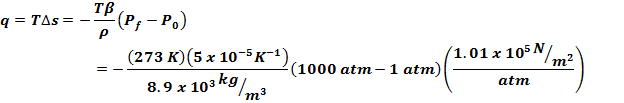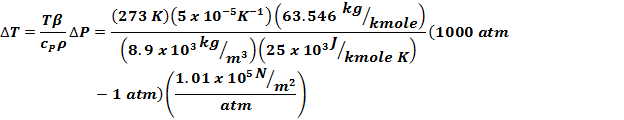|
|
|
|
P 6 – 22 The pressure on a block of
copper at a temperature of 0°C is increased isothermally and reversibly from
1 atm to 1000 atm. Assume that β,
k, and ρ are constant and equal respectively to
5 x 10-5 K-1 , 8 x 10-12 N-1 m2,
and 8.9 x 103 kg m-3 .
Calculate (a) the work done on the coper per kilogram, and (b) the
heat evolved. (c) How do you account
for the fact that the heat evolved is greater than the work done? (d) What would be the rise in temperature
of the copper, if the compression were adiabatic rather than isothermal? Explain approximations made. |
|
|
|
|
|
Calculate (a) the work done on the coper per
kilogram |
|
|
|
|
|
For
dv use |
|
|
|
|
|
|
|
|
|
|
|
integrating |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Calculate
(b) the heat evolved |
|
|
|
|
|
Heat
evolved can be found from q = TDs, Eq(6-24) gives us |
|
|
|
|
|
|
|
|
So
we can write Tds as follows |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Now
integrating |
|
|
|
|
|
|
|
|
|
|
|
Heat
evolved then is |
|
|
|
|
|
|
|
|
|
|
|
|
|
(c)
How do you account for the fact that the heat evolved is greater than the
work done? |
|
|
|
|
|
|
|
|
|
|
(d)
What would be the rise in temperature of the copper, if the compression were
adiabatic rather than isothermal?
Explain approximations made. |
|
|
|
|
|
Eq
(6-31) indicates |
|
|
|
|
|
Adiabatic
means ds = 0 so |
|
|
|
|
|
|
|
|
|
|
|
Integrating |
|
|
|
|
|
Need
cP, so use Figure 3-10, use
cP = 25 x 103 J/kmole K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|