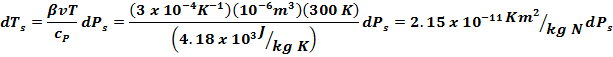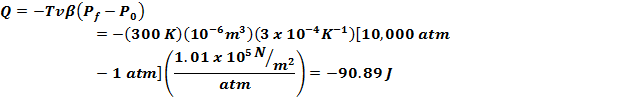P 6 – 26 The isothermal compressibility of water is 50 x 10^-6 atm^-1 and c_P = 4.18 x 10³ J kg^-1 K^-1. Other properties of water are given in the previous problem. Calculate the work done as the pressure on 1 g of water in a hydraulic press is increased reversibly from 1 atm to 10,000 atm (a) isothermally, (b) adiabatically, (c) Calculate the heat evolved in (a) the isothermal process.

Calculate the work done as the pressure on 1 g of water in a hydraulic press is increased reversibly from 1 atm to 10,000 atm (a) isothermally,

From section 6-9 we are reminded that dv can be written as

So work can be found from

Isothermal reduces this to

From problem 6-25, if we assume the temperature is 4°C, then v = 1 cm³ = 10^-6 m³

So work per gram is

Calculate the work done as the pressure on 1 g of water in a hydraulic press is increased reversibly from 1 atm to 10,000 atm (b) adiabatically,

Again work is found from

We need to find dT for adiabatic, from eq (6-34)

But β = 3 x 10^-4 K^-1 for water at 300 K, so

Compared to dP_s, we can ignore this term. So work can now be found from

We now must replace k with k_s = k/g

Eq (6-12) gives us

So c_P = c_v and g = 1 so k_s = k, so the work adiabatically is the same as the work isothermally.

(c) Calculate the heat evolved in (a) the isothermal process.

Eq (6-31)

Since isothermal dT = 0

Integrating

Thus the heat evolved isothermally is