|
|
|
*52.  Two geological field teams are working
in a remote area. A global positioning system (GPS) tracker at their base
camp shows the location of the first team as 38 km away, 19°
north of west, and the second team as 29 km away, 35° east of north. When the
first team uses its GPS to check the position of the second team, what does
the GPS give for the second team’s (a) distance from them and (b)
direction, measured from due east? Two geological field teams are working
in a remote area. A global positioning system (GPS) tracker at their base
camp shows the location of the first team as 38 km away, 19°
north of west, and the second team as 29 km away, 35° east of north. When the
first team uses its GPS to check the position of the second team, what does
the GPS give for the second team’s (a) distance from them and (b)
direction, measured from due east?
|
|
|
|
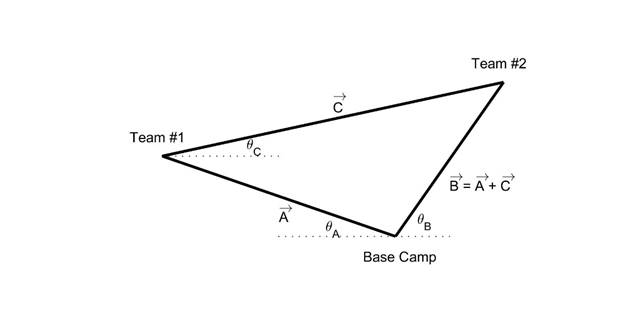
The Situation is as shown
|
|
|
|
We are given vectors  and and  . We need to find vector . We need to find vector 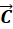 , which from the diagram could be written as , which from the diagram could be written as
 . So we can find this if we find x and
y-components and then find C’s x and y-components. . So we can find this if we find x and
y-components and then find C’s x and y-components.
|
|
|
|
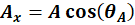
|
|
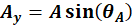
|
|
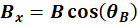
|
|
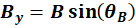
|
|
From the way the angles are
provided in the problem,  is given as 19° North of West, this will be written as 180°-19° as 180° is due West and subtracting moves you North of West. is given as 19° North of West, this will be written as 180°-19° as 180° is due West and subtracting moves you North of West.  is given as 35° East of North, so it will be written as 90°-35°. So our components are: is given as 35° East of North, so it will be written as 90°-35°. So our components are:
|
|
|
|
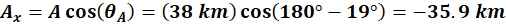
|
|
Note, since this points west, on our
coordinate system it should be negative!
|
|

|
|
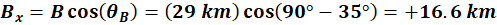
|
|
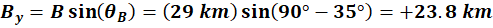
|
|
|
|
As mentioned earlier we know  , So we find the x
and y-components of , So we find the x
and y-components of 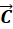 as follows: as follows:
|
|
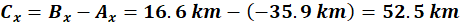
|
|
|
|
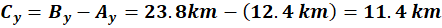
|
|
|
|
Now we can use the Pythagorean
theorem to find magnitude and direction of 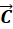
|
|
|
|
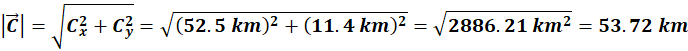
|
|
|
|
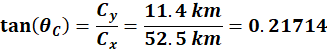
|
|
|
|
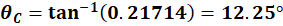
|
|
|
|
So the displacement vector
from Team #1 to Team #2 is
|
|
|
|
|
|
|
|
|
|
Please send any comments or questions about this page to ddonovan@nmu.edu
|
|
This page last updated on
January 11, 2020
|
|
|
|
|
