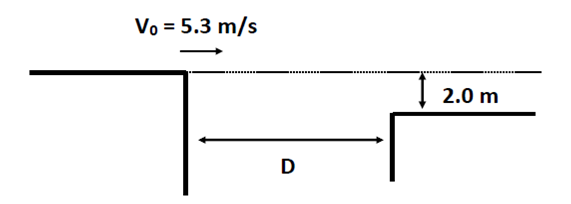
24.  A criminal is escaping across a rooftop and runs off the roof horizontally at a speed of 5.3 m/s, hoping to land on the roof of an adjacent building. Air resistance is negligible. The horizontal distance between the two buildings is D, and the roof of the adjacent building is 2.0 m below the jumping-off point. Find the maximum value for D.

We know the following variables:

= -

 

 

No air Resistance

 

 

=

 

 

Initial velocity is horizontal

y

= - 2.0 m

 

 

 

So, D is as wide as time allows.  We get time from how long does it take an object to fall from rest a total of 2.0 m?

Solve for t

Plug in t and solve for D

 

 

 

Please send any comments or questions about this page to ddonovan@nmu.edu

This page last updated on January 11, 2020