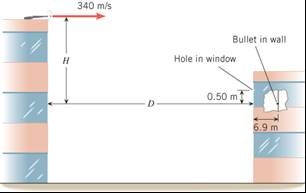
**49. ssm From the top of a tall building, a gun is fired. The bullet leaves the gun at a speed of 340 m/s, parallel to the ground. As the drawing shows, the bullet puts a hole in a window of another building and hits the wall that faces the window. Using the data in the drawing, determine the distances D and H, which locate the point where the gun was fired. Assume that the bullet does not slow down as it passes through the window.

 

 

We break up the motion into two parts, part 1 is the bullet traveling from the roof of the building on the left to hitting the window in the building on the right.  So t1 is the time for the bullet to fall a distance (H-0.50 m).  Part 2 is the bullet traveling from the window to the wall in the building on the right.  So t2 is the time for the bullet to travel horizontally (6.9 m) and to fall vertically (0.50 m).

 

We know these kinematical variables, ,  , , and

 .

 

Part 1

Horizontal motion

 

Vertical motion

 

Part 2

Horizontal motion

 remains constant as we are ignoring air resistance and assuming the window has no effect on the bullet’s speed when it passes through it.

Vertical motion

 

For this part, there is initial y velocity if we consider only the window to the wall.  The bullet having fallen (H - 0.50m) it possess vertical velocity at that point, so we call it

 

From the horizontal motion we can find time t2

 

 

 

Now we know everything in the vertical equation except the , so we can rearrange and solve for that.

 

 

 

 

 

Now that we know the vertical velocity of the bullet when it hits the window, we also know the initial velocity vertically is zero.  So we can use the relationship

 

This allows us to solve for t1

Recall what we found earlier

 

 

 

 

 

 

Please send any comments or questions about this page to ddonovan@nmu.edu

This page last updated on January 11, 2020