|
**93. ssm A penguin slides at a constant velocity of 1.4 m/s down an
icy incline. The incline slopes above the horizontal at an angle of 6.9°. At
the bottom of the incline, the penguin slides onto a horizontal patch of ice.
The coefficient of kinetic friction between the penguin and the ice is the
same for the incline as for the horizontal patch. How much time is required
for the penguin to slide to a halt after entering the horizontal patch of
ice? |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
We need to break this into two
parts. Part 1 we have the penguin
sliding down the incline with a constant speed of 1.4 m/s. At the bottom of the incline
we have the same speed and now we want to know how long will it take to stop
it on the flat ice. So
we know our final speed is zero. We
know our acceleration from sum of the forces and we can use kinematics to
find the time. |
|||||||||||||||||||
|
The kinematic equation we need
is |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
Solving for t |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
We get a from Newton’s second
law |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
Solving for a |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
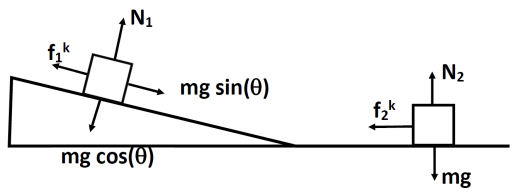
We can get fk
from summing equations on the incline. |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
Since there is no motion in
the perpendicular direction of the bicyclist on the hill, there is no
acceleration perpendicular. |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
Since the penguin is traveling
at constant speed down the incline, there is no acceleration down the
incline. |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
But we know |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
Solving for |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
So now we have |
|||||||||||||||||||
|
Now sum forces on the flat
part |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
Since penguin is not moving
vertically on flat ice, acceleration vertically is zero. |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
So |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|||||||||||||||||||
|
|