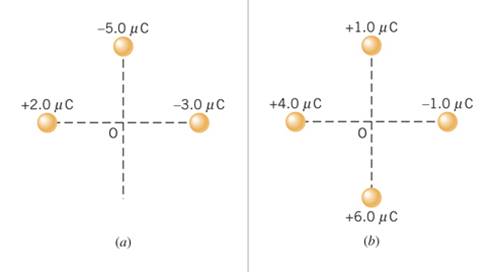
34. The drawing shows two situations in which charges are placed on the x and y axes. They are all located at the same distance of 6.1 cm from the origin O. For each of the situations in the drawing, determine the magnitude of the net electric field at the origin.

We can use the principle of Linear Superposition which says the net electric field is the sum of the individual electric fields.

For Part (a) we have

direction since it is a positive charge.

direction since it is a negative charge.

direction since it is a negative charge.

So we have two perpendicular vectors, use Pythagorean theorem

For Part (a)

For Part (b) Similarly we have

direction since it is a positive charge.

direction since it is a positive charge.

direction since it is a negative charge.

direction since it is a positive charge.

Which is what we found in part (a) so the final answer is also

For both parts (a) and (b)

	Dr. Donovan's Classes Page	Dr. Donovan's PH 202 Homework Page
Dr. Donovan's Main Web Page	NMU Physics Department Web Page	NMU Main Page

Please send any comments or questions about this page to ddonovan@nmu.edu

This page last updated on June 4, 2018