|
|
|||||||||||||||||||
|
**102.
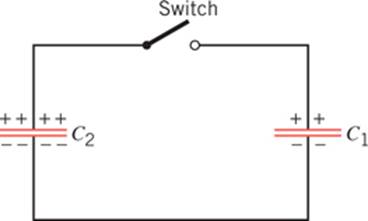
The drawing shows two capacitors that are fully charged (C1 = 2.00 µF, q1 = 6.00 µC; C2 = 8.00 µF, q2 = 12.0 µC). The switch is closed, and charge flows until
equilibrium is reestablished (i.e., until both capacitors have the same
voltage across their plates). Find the resulting voltage across either
capacitor. |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
When the switch is thrown we have two capacitors in parallel. SO we can
determine what the capacitance is and the charge will be the sum of the
original charges since there is no source or sink of charges. Then we can determine what the voltage
across will be and that will be the voltage on both capacitors. If we wish we
could then determine how much charge remains on each capacitor. |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
Not asked for but let’s see
the final charges on each |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
As it should! |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|||||||||||||||||||
|
|