*9.  The drawing shows a parallel plate capacitor that is moving with a speed of 32 m/s through a 3.6-T magnetic field. The velocity  is perpendicular to the magnetic field. The electric field within the capacitor has a value of 170 N/C, and each plate has an area of

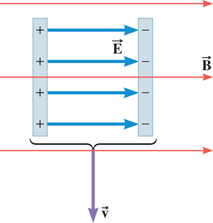
7.5 x 10-4 m2. What is the magnetic force (magnitude and direction) exerted on the positive plate of the capacitor?

 

w1111

 

The magnetic force is given by

 

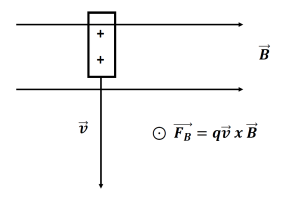
So consider the positive plate only in the figure below and the relationship of the vectors , and , then the right hand rules as indicated provides that the force on the positive plate would be out of the paper.  Additionally consider that since the negative plate is negative charge the force on the negative plate would be into the paper!

So to calculate the magnitude of the force we need the charge on the positive plate.  We have already the velocity and magnetic field strength.  We also have the electric field between the plates.  The relationship for that is

 

So

 

Since the vectors , and  are perpendicular the angle between them is 90° so the magnitude of the magnetic force is

 

 

 

 

Please send any comments or questions about this page to ddonovan@nmu.edu

This page last updated on June 21, 2018