|
|
|||||||||||||||||||
|
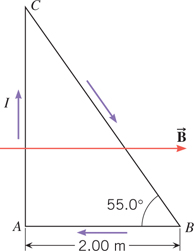
37. A loop of wire has the
shape of a right triangle (see the drawing) and carries a current of I = 4.70 A. A uniform magnetic
field is directed parallel to side AB and has a magnitude of
1.80 T. (a) Find the magnitude and direction of
the magnetic force exerted on each side of the triangle. (b) Determine the magnitude of
the net force exerted on the triangle. |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
The magnetic force on a
current carrying wire in a magnetic field can be written as |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
For segment AB, |
|||||||||||||||||||
|
Since the current is
anti-parallel to the magnetic field, the cross product is zero and the
magnetic force is also zero. |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
For segment AC, |
|||||||||||||||||||
|
The current is perpendicular
to the magnetic field, by using the right hand rule for the cross product the
direction of the force is into the paper! |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
For segment BC, |
|||||||||||||||||||
|
The current is at an angle to
the magnetic field so we have |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
The direction this time by the
right hand rule is out of the paper so the force on BC is |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
The total force then is |
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|
|||||||||||||||||||
|
|||||||||||||||||||
|
|