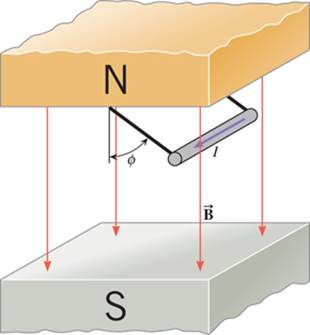
*40.   A horizontal wire is hung from the ceiling of a room by two massless strings. The wire has a length of 0.20 m and a mass of 0.080 kg. A uniform magnetic field of magnitude 0.070 T is directed from the ceiling to the floor. When a current of I = 42 A exists in the wire, the wire swings upward and, at equilibrium, makes an angle φ with respect to the vertical, as the drawing shows. Find (a) the angle φ and (b) the tension in each of the two strings.

 

w1118

Free Body Diagram for wire, note magnetic force result of right hand rule!

Better if we break tension up into x and y components

Now sum forces in each direction and remember this is in equilibrium and not moving.

 

 

 

Solve for the two tension components

 

 

 

We can find the angle by using the tangent relation

 

 

 

Then the total tension in the strings is found from

 

 

So since there are two strings, the tension in each is one half the total tension

 

 

 

 

Please send any comments or questions about this page to ddonovan@nmu.edu

This page last updated on June 21, 2018