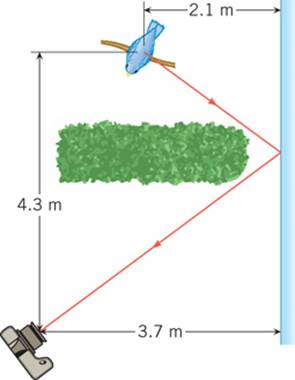
3. ssm You are trying to photograph a bird sitting on a tree branch, but a tall hedge is blocking your view. However, as the drawing shows, a plane mirror reflects light from the bird into your camera. For what distance must you set the focus of the camera lens in order to snap a sharp picture of the bird’s image?

Consider in the diagram below where the image of the bird is

The focal length is the hypotenuse of the right triangle below in the diagram.

Alternatively if you failed to see this, you could do a longer more geometry based solution.

The diagram below shows the angles we know. The law of reflection makes the middle two q₁’s and the other two q₁’s are equal from alternate angles of parallel lines.

Since the upper and lower triangle have the same three angles (q₁. 90°, and 90°- q₁) so we know

And

We can solve for one of them

The distance we must focus the camera is the sum of the two hypotenuse

We get these hypotenuse using the other two sides.

	Dr. Donovan's Classes Page	Dr. Donovan's PH 202 Homework Page
Dr. Donovan's Main Web Page	NMU Physics Department Web Page	NMU Main Page

Please send any comments or questions about this page to ddonovan@nmu.edu

This page last updated on June 27, 2018