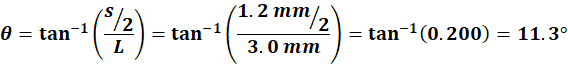47. ssm The wavelength of the laser beam used in a compact disc player is 780 nm. Suppose that a diffraction grating produces first-order tracking beams that are 1.2 mm apart at a distance of 3.0 mm from the grating. Estimate the spacing between the slits of the grating.

For a diffraction grating the condition for bright spots is given by

Since we want the first order brights. Solve for the grating spacing

So we need the angle. We know the tangent is

We need the angle between the central max and the first bright. So we need half the spacing of the two first order brights.

Now we can plug in for grating spacing

	Dr. Donovan's Classes Page	Dr. Donovan's PH 202 Homework Page
Dr. Donovan's Main Web Page	NMU Physics Department Web Page	NMU Main Page

Please send any comments or questions about this page to ddonovan@nmu.edu

This page last updated on July 14, 2018