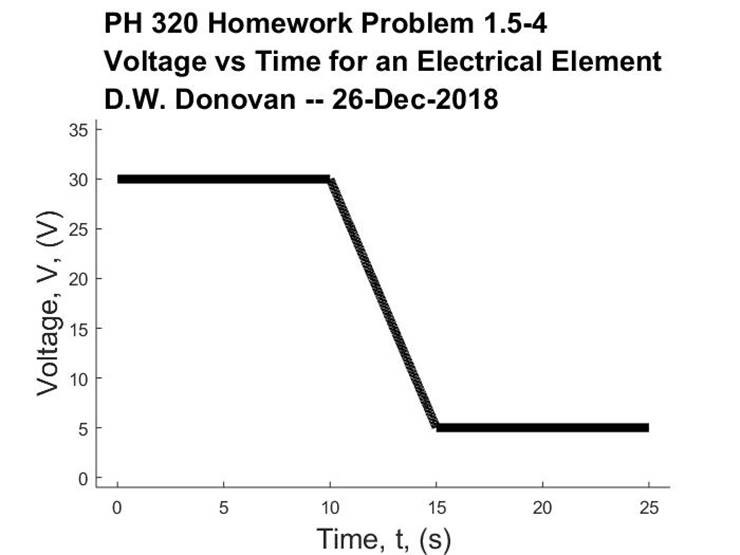
P 1.5-4 The current through and voltage across an element vary with time as shown in Figure P 1.5-4. Sketch the power delivered to the element for t > 0. What is the total energy delivered to the element between t = 0 and t = 25 s? The element voltage and current adhere to the passive convention.

Figure P 1.5-4

First we need to get equations from these two graphs. As before, we will use two point forms of lines.

For the voltage curve we have two flat lines so we already know

Need Eq

V is in V when t is in s.

Need to get equation for between 10 and 15 s. Use points (10, 30) and (15, 5)

Now get current. We have two lines use the three points (0,0) (15, 30) and (25, 0)

For

For

So our equations are

Voltage (V is in V when t is in s)

Current (I is in A when t is in s)

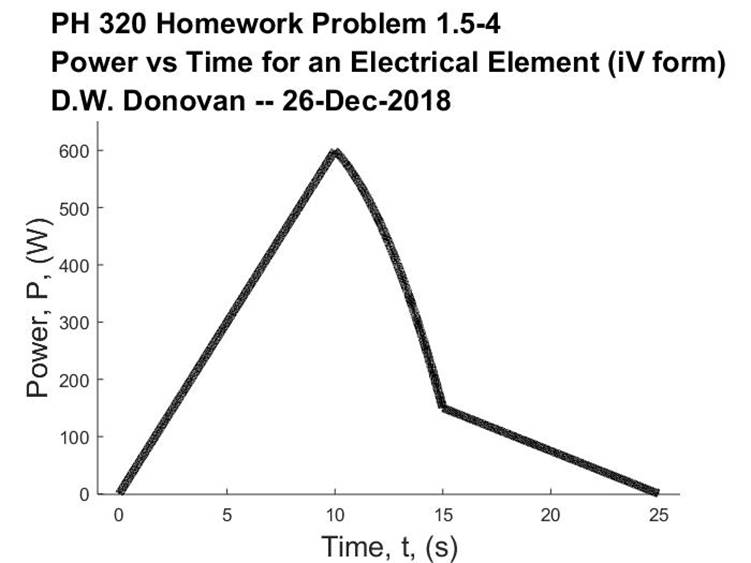
Power is i(t)V(t) so we get

P is in W when t is in s.

We can plug these into MATLAB and get the plot. To get the energy we now use

P is in W when t is in s.

MATLAB Plots and Code follows:

%Program to plot out Current vs time for Homework Problem 1.5-4.

%Version 2018-12-26 DW Donovan

clear all;

ta = [1e-9:0.001:10]';

tb = [10.00:0.001:15]';

tc = [15.00:0.001:25]';

x = [ta' tb' tc'];

Va = 30*ta./ta;

Vb = -5*tb + 80;

Vc= 5*tc./tc;

Vy = [Va' Vb' Vc'];

ia = 2*ta;

ib = 2*tb;

ic = -3*tc+75;

iy =[ia' ib' ic'];

P1a = Va.*ia;

P1b = Vb.*ib;

P1c = Vc.*ic;

P1y = [P1a' P1b' P1c'];

P2a = 60*ta;

P2b = -10*tb.^2 + 160*tb;

P2c = -15*tc + 375;

P2y = [P2a' P2b' P2c'];

%Energy Calculation

Ua = P1a'*(ta./ta)*.001

Ub = P1b'*(tb./tb)*.001

Uc = P1c'*(tc./tc)*.001

Utot = Ua + Ub + Uc

%{

Energy Answers

Ua = 2.9997e+03

Ub = 2.0837e+03

Uc = 750.0750

Utot = 5.8335e+03

%}

% Plots

tt1 = 'PH 320 Homework Problem 1.5-4';

ttn = 'D.W. Donovan -- ';

tnl = '\newline';

xl = 'Time, t, (s)';

tt2a = 'Voltage vs Time for an Electrical Element';

ttfa = [tt1 tnl tt2a tnl ttn date];

yla = 'Voltage, V, (V)';

tt2b = 'Current vs Time for an Electrical Element';

ttfb = [tt1 tnl tt2b tnl ttn date];

ylb = 'Current, i, (A)';

tt2c = 'Power vs Time for an Electrical Element (iV form)';

ttfc = [tt1 tnl tt2c tnl ttn date];

ylc = 'Power, P, (W)';

tt2d = 'Power vs Time for an Electrical Element (P Eq Form)';

ttfd = [tt1 tnl tt2d tnl ttn date];

yld = 'Power, P, (W)';

sp = 1;

axxmin = min(x)-sp;

axxmax = max(x) + sp;

axyminV = min(Vy) - 5 - sp;

axymaxV = max(Vy) + 5 + sp;

axymini = min(iy) - sp;

axymaxi = max(iy) + 5 + sp;

axyminP1 = min(P1y) - sp;

axymaxP1 = max(P1y) + 50 + sp;

axyminP2 = min(P2y) - sp;

axymaxP2 = max(P2y) + 50 + sp;

figure

hold on

plot(ta, Va,'k-','LineWidth',5)

plot(tb, Vb,'k-','LineWidth',5)

plot(tc, Vc,'k-','LineWidth',5)

title (ttfa,'FontSize', 16)

xlabel(xl, 'FontSize', 16)

ylabel(yla, 'FontSize', 16)

axis([axxmin axxmax axyminV axymaxV])

figure

hold on

plot(ta, ia,'k-','LineWidth',5)

plot(tb, ib,'k-','LineWidth',5)

plot(tc, ic,'k-','LineWidth',5)

title (ttfb,'FontSize', 16)

xlabel(xl, 'FontSize', 16)

ylabel(ylb, 'FontSize', 16)

axis([axxmin axxmax axymini axymaxi])

figure

hold on

plot(ta, P1a,'k-','LineWidth',5)

plot(tb, P1b,'k-','LineWidth',5)

plot(tc, P1c,'k-','LineWidth',5)

title (ttfc,'FontSize', 16)

xlabel(xl, 'FontSize', 16)

ylabel(ylc, 'FontSize', 16)

axis([axxmin axxmax axyminP1 axymaxP1])

figure

hold on

plot(ta, P2a,'k-','LineWidth',5)

plot(tb, P2b,'k-','LineWidth',5)

plot(tc, P2c,'k-','LineWidth',5)

title (ttfd,'FontSize', 16)

xlabel(xl, 'FontSize', 16)

ylabel(yld, 'FontSize', 16)

axis([axxmin axxmax axyminP2 axymaxP2])

Dr. Donovan's Classes Page	Dr. Donovan's PH 320 Homework Page	PH 320 Homework Chapter 1 Page
Dr. Donovan's Main Web Page	NMU Physics Department Web Page	NMU Main Page

Please send any comments or questions about this page to ddonovan@nmu.edu

This page last updated on December 26, 2018