P 5.5-12 Use Norton’s theorem to formulate a general expression for the current i in terms of the variable resistance R shown in Figure P 5.5-12.

Answer: i = 20/(8 + R) A

Figure P 5.5-12

Find the Norton equivalent circuit to everything except resistor R. First deactivate the voltage source and find the equivalent resistance between points a and b.

Rearrange this to make identifying the resistor relationships easier. This is same circuit electrically

Now it is obvious that the 8 Ω and the 16 Ω are in series which becomes a 24 Ω resistance which is in parallel with a 12 Ω resistor. SO the equivalent resistance is

So

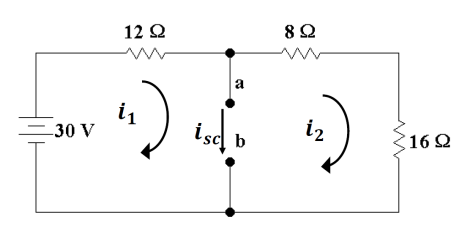
Now we have to find the short circuit current between a and b

I have set up and labeled two mesh currents. The equations are

ans

The second equation gives while the first equation provides

So our equivalent circuit can be drawn as

So we can get i from current division

Dr. Donovan's Classes Page	Dr. Donovan's PH 320 Homework Page	PH 320 Homework Chapter 5 Page
Dr. Donovan's Main Web Page	NMU Physics Department Web Page	NMU Main Page

Please send any comments or questions about this page to ddonovan@nmu.edu

This page last updated on March 8, 2019