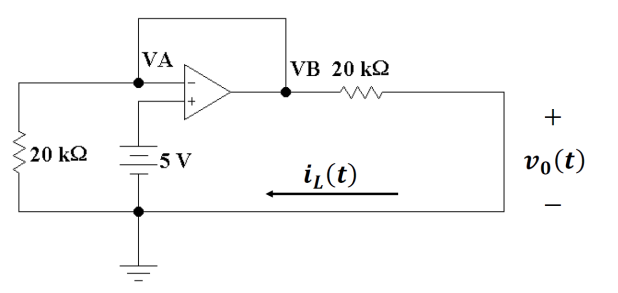
P 8.3-6 The circuit shown in Figure P 8.3-6 is at steady state before the switch opens at time

t = 0. Determine the voltage, v_o(t), for t > 0.

Answer: v_o(t) = 5e^–4000t V for t > 0

Figure P 8.3-6

With the switch closed the equilibrium circuit for t < 0, The closed switch shorts out the resistor and long term the inductor looks like a short-circuit, so the annotated circuit looks like:

Rules of ideal op-amps, mean VA = 5 V and VB = 5 V also. Therefore, iL is

Once the switch opens the annotated circuit looks like now:

In this case, VA remains 5 V, but now the current goes from ground up through the 20 kΩ resistor on the left. So clearly the voltage across the 20 kΩ resistor is 5 V. that means as that current passes through the 20 kΩ resistor on top, you must get another 5 V, since the current in that resistor is going from left to right, VB now is +10 V! This changes the current through the short circuit inductor is

and

So the current through the inductor is found from the general form

The voltage across the inductor is found from

Dr. Donovan's Classes Page	Dr. Donovan's PH 320 Homework Page	PH 320 Homework Chapter 8 Page
Dr. Donovan's Main Web Page	NMU Physics Department Web Page	NMU Main Page

Please send any comments or questions about this page to ddonovan@nmu.edu

This page last updated on July 1, 2019