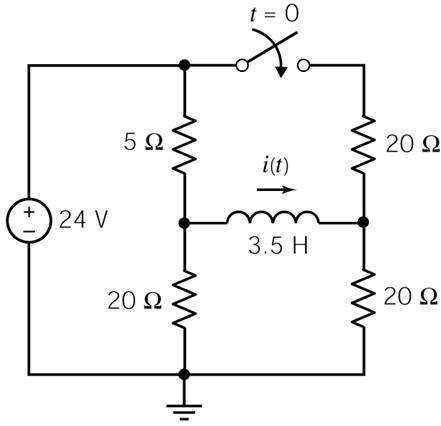
P 8.3-20 The circuit shown in Figure P 8.3-20 is at steady state before the switch closes. Determine i(t) for t ≥ 0.

 

P8_3_20

Figure P 8.3-20

 

The standard form of the current in the inductor is

 

 

So just before the switch is thrown the circuit is in steady state, so the inductor looks like a short circuit and the whole circuit looks like

The two 20 Ω resistors are in parallel and their effective resistance is

 

 

The total effective resistance is therefore 15 Ω as the 5 Ω and 10 Ω are in series, so the current in the circuit is

 

 

Now since the two 20 Ω resistors are in parallel and equal in magnitude, the current will divide in half and so the

 

After the switch is thrown and the enough time passes for steady state, the circuit would now look like

Again find the effective resistance so we can find the total current.  Clearly the 5 Ω and the upper right 20 Ω resistors are in parallel and we get an effective resistance of

 

 

Again having two 20 Ω resistors in series provides a 10 Ω resistance and so we have a circuit now that looks like this

Therefore the total resistance is 14 Ω and the total current is

 

 

Again the two 20 Ω resistors split the current evenly so the long term current is

 

 

However, the 5 Ω and the 20 Ω resistor will split the current with 4/5’s going through the

5 Ω and 1/5 going through the 20 Ω.  So the current flowing through the inductor is

 

 

Alternatively could set up and solve mesh currents

So Mesh equations can be written

 

 

 

 

Plugging into MATLAB yields

 

ans =

 

    'i1 = 1.7143 A'

    'i2 = 0.34286 A'

    'i3 = 0.85714 A'

    'iL = 0.51429 A'

 

Similar to what we got from current division

 

Now we need Thevenin resistance which would look like

This can be redrawn as

This can be simplified to

So the Thevenin resistance is

And

 

So plugging into standard from for current we get

 

 

 

MATLAB code follows:

 

%Program to solve PH 320 Homework Problem P8.3-20

%version 2019-07-09 DW Donovan

clear all;

 

RR = [(5 + 20) -5 -20;

    -5 (5 + 20) 0;

    -20 0 (20 +20)];

 

VV = [24 0 0]';

 

II = RR\VV;

i1 = II(1);

i2 = II(2);

i3 = II(3);

iL = i3-i2;

 

 

ans ={['i1 = ' num2str(i1) ' A']; ['i2 = ' num2str(i2) ' A'];

    ['i3 = ' num2str(i3) ' A']; ['iL = ' num2str(iL) ' A']};

 

ans

 

%{

ans =

 

    'i1 = 1.7143 A'

    'i2 = 0.34286 A'

    'i3 = 0.85714 A'

    'iL = 0.51429 A'

%}

 

 

Please send any comments or questions about this page to ddonovan@nmu.edu

This page last updated on July 9, 2019